library(groupedHyperframe.random)
# Loading required package: groupedHyperframe3 Simulation
The examples in Chapter 3 require
search path & loadedNamespaces on author’s computer
search()
# [1] ".GlobalEnv" "package:groupedHyperframe.random" "package:groupedHyperframe" "package:stats" "package:graphics"
# [6] "package:grDevices" "package:utils" "package:datasets" "package:methods" "Autoloads"
# [11] "package:base"
loadedNamespaces() |> sort.int()
# [1] "abind" "base" "cli" "cluster" "codetools" "compiler" "datasets"
# [8] "deldir" "digest" "doParallel" "dplyr" "evaluate" "farver" "fastmap"
# [15] "fastmatrix" "foreach" "generics" "geomtextpath" "GET" "ggplot2" "glue"
# [22] "goftest" "graphics" "grDevices" "grid" "gridExtra" "groupedHyperframe" "groupedHyperframe.random"
# [29] "gtable" "htmltools" "htmlwidgets" "iterators" "jsonlite" "knitr" "lattice"
# [36] "lifecycle" "magrittr" "MASS" "Matrix" "matrixStats" "methods" "nlme"
# [43] "otel" "parallel" "patchwork" "pillar" "pkgconfig" "polyclip" "pracma"
# [50] "R6" "RColorBrewer" "rlang" "rmarkdown" "rstudioapi" "S7" "scales"
# [57] "SpatialPack" "spatstat.data" "spatstat.explore" "spatstat.geom" "spatstat.random" "spatstat.sparse" "spatstat.univar"
# [64] "spatstat.utils" "splines" "stats" "survival" "systemfonts" "tensor" "textshaping"
# [71] "tibble" "tidyselect" "tools" "utils" "vctrs" "viridisLite" "xfun"
# [78] "yaml"3.1 Simulated Point-Pattern
Function .rppp() (Chapter 51) simulates superimposed point-patterns (ppp.object, Chapter 35) via vectorized parameterization, which is supported in the parameter-specification of both the random point-pattern and the random marks.
Listing 3.1 simulates an \(x\)- and \(y\)-coordinates only, two superimposed Matérn (1986)’s cluster processes \((\kappa, \mu, s)\) with parameters \((\kappa_1, \mu_1, s_1) = (10,8,.15)\) and \((\kappa_2, \mu_2, s_2) = (5,4,.06)\) using a vectorized parameterization of Table 3.1.
kappa \(\kappa\) |
mu \(\mu\) |
scale \(s\) |
|
|---|---|---|---|
| Vecterization | \((\kappa_1, \kappa_2)\) | \((\mu_1, \mu_2)\) | \((s_1, s_2)\) |
| Restriction | \(\kappa_i>1\) | \(\mu_i>1\) | \(s_i>0\) |
set.seed(12); r = .rppp(rMatClust(kappa = c(10, 5), mu = c(8, 4), scale = c(.15, .06)))
# Point-pattern simulated by `spatstat.random::rMatClust()`
# Listing 3.2 simulates two superimposed marked point-patterns,
- one marked point-pattern with
- \(x\)- and \(y\)-coordinates by Matérn (1986)’s cluster process with parameters \((\kappa_1,\mu_1,s_1) = (10,8,.15)\);
- log-normal \((\log\mu, \log\sigma)\) marks with parameters \((\log\mu_1,\log\sigma_1)=(3,.4)\);
- negative-binomial \((r, p)\) marks with parameters \((r,p)=(4,.3)\).
- another marked point-pattern with
- \(x\)- and \(y\)-coordinates by Matérn (1986)’s cluster process with parameters \((\kappa_2,\mu_2,s_2) = (5,4,.06)\);
- log-normal marks with parameters \((\log\mu_2,\log\sigma_2)=(5,.2)\)
- negative-binomial marks with parameters \((r,p)=(4,.3)\).
using a vectorized parameterization of Table 3.2.
kappa \(\kappa\) |
mu \(\mu\) |
scale \(s\) |
meanlog \(\log\mu\) |
sdlog \(\log\sigma\) |
size \(r\) |
prob \(p\) |
|
|---|---|---|---|---|---|---|---|
| Vec. | \((\kappa_1, \kappa_2)\) | \((\mu_1, \mu_2)\) | \((s_1, s_2)\) | \((\log\mu_1, \log\mu_2)\) | \((\log\sigma_1, \log\sigma_2)\) | \((r_1, r_2)\) | \((p_1, p_2)\) |
| Res. | \(\kappa_i>1\) | \(\mu_i>1\) | \(s_i>0\) | (none) | \(\log\sigma_i>0\) | \(r_i>0\) | \(0<p_i<1\) |
set.seed(25); r1 = .rppp(
rMatClust(kappa = c(10, 5), mu = c(8, 4), scale = c(.15, .06)),
rlnorm(meanlog = c(3, 5), sdlog = c(.4, .2)),
rnbinom(size = 4, prob = .3) # shorter arguments recycled
)
# Point-pattern simulated by `spatstat.random::rMatClust()`
# Mark simulated by `stats::rlnorm()`
# Mark simulated by `stats::rnbinom()`Listing 3.3 simulates two superimposed point-patterns,
- one marked point-pattern with
- \(x\)- and \(y\)-coordinates by Poisson point-pattern \(\lambda\) with parameter \(\lambda_1=3\),
- log-normal marks with parameters \((\log\mu_1,\log\sigma_1)=(3,.4)\);
- negative-binomial marks with parameters \((r_1,p_1)=(4,.3)\).
- another marked point-pattern with
- \(x\)- and \(y\)-coordinates by Poisson point-pattern with parameters \(\lambda_2=6\)
- log-normal marks with parameters \((\log\mu_2,\log\sigma_2)=(5,.2)\)
- negative-binomial marks with parameters \((r_2,p_2)=(6,.1)\).
using a vectorized parameterization of Table 3.3.
lambda \(\lambda\) |
meanlog \(\log\mu\) |
sdlog \(\log\sigma\) |
size \(r\) |
prob \(p\) |
|
|---|---|---|---|---|---|
| Vecterization | \((\lambda_1, \lambda_2)\) | \((\log\mu_1, \log\mu_2)\) | \((\log\sigma_1, \log\sigma_2)\) | \((r_1, r_2)\) | \((p_1, p_2)\) |
| Restriction | \(\lambda_i>0\) | (none) | \(\log\sigma_i>0\) | \(r_i>0\) | \(0<p_i<1\) |
set.seed(62); r2 = .rppp(
rpoispp(lambda = c(3, 6)),
rlnorm(meanlog = c(3, 5), sdlog = c(.4, .2)),
rnbinom(size = c(4, 6), prob = c(.3, .1))
)
# Point-pattern simulated by `spatstat.random::rpoispp()`
# Mark simulated by `stats::rlnorm()`
# Mark simulated by `stats::rnbinom()`Listing 3.4 superimposes the simulated (marked) point-patterns r1 and r2 (Listing 3.2, Listing 3.3).
spatstat.geom::superimpose.ppp(r1, r2)
# Marked planar point pattern: 140 points
# Mark variables: rlnorm, rnbinom
# window: rectangle = [0, 1] x [0, 1] units3.2 Simulated Grouped Hyper Data Frame
Function grouped_rppp() (Chapter 45) simulates a grouped hyper data frame containing one-and-only-one point-pattern (ppp) hypercolumn (Chapter 2) via matrix parameterization, which is supported in the subject-specific parameter-specification of both the random point-pattern and the random marks.
3.2.1 with Superimposed Matérn (1986)’s Cluster Processes
Table 3.4 outlines the three steps described in Section 3.2.1,
| To Simulate | Primary Function | |
|---|---|---|
| 1. | subject-specific parameters of (marked) point-patterns, based on multivariate normal distribution, Listing 3.5 | mvrnorm2() (Chapter 47) |
| 2. | number of (marked) point-patterns per subject, Listing 3.7 | base::sample() |
| 3. | grouped hyper data frame with one-and-only-one ppp-hypercolumn, Listing 3.8 |
grouped_rppp() (Chapter 45) |
Consider two superimposed Matérn (1986)’s cluster processes, each with one log-normal mark. The population parameters are
- \(x\)- and \(y\)-coordinates by Matérn (1986)’s cluster process \((\kappa_1,\mu_1,s_1) = (3,10,.4)\), with a log-normal mark \((\log\mu_1,\log\sigma_1)=(3,.4)\)
- \(x\)- and \(y\)-coordinates by Matérn (1986)’s cluster process \((\kappa_2,\mu_2,s_2) = (2,5,.2)\), with a log-normal mark \((\log\mu_2,\log\sigma_2)=(5,.2)\)
Listing 3.5 simulates for three (3L) subjects (e.g., patients). The subject-specific parameters deviate from the population parameters under a multivariate normal distribution specified by the standard deviation(s) \(\sigma\) of the subject-specific random effects, i.e., \(\sigma_\kappa=.2\), \(\sigma_\mu=.5\), \(\sigma_s=.05\), \(\sigma_{\log\mu}=.1\) and \(\sigma_{\log\sigma}=.01\), as well as the restrictions in Table 3.2.
p_Matern
set.seed(39); p_Matern = mapply(
FUN = mvrnorm2,
mu = list(kappa = c(3,2), mu = c(10,5), scale = c(.4,.2), meanlog = c(3,5), sdlog = c(.4,.2)),
sd = list(kappa = .2, mu = .5, scale = .05, meanlog = .1, sdlog = .01),
MoreArgs = list(n = 3L, row.prefix = 'Subj', col.prefix = 'Pattern'),
SIMPLIFY = FALSE
) |>
within.list(expr = {
kappa = pmax(kappa, 1 + .Machine$double.eps)
mu = pmax(mu, 1 + .Machine$double.eps)
scale = pmax(scale, .Machine$double.eps)
sdlog = pmax(sdlog, .Machine$double.eps)
})Listing 3.6 shows the subject-specific parameters p_Matern as a list of matrices, where each matrix represents one parameter used in generating the random marked point-patterns. In these matrices,
- Each row corresponds to a subject; i.e., each matrix in
p_Materncontains three (3L) rows, one for each of the three (3L) subjects; - Each column corresponds to a random generation parameter for each superimposed marked point-pattern; i.e., each matrix in
p_Materncontains two (2L) columns, one for each of the two (2L) marked Matérn (1986)’s cluster processes to be superimposed.
p_Matern (Listing 3.5)
p_Matern
# $kappa
# Pattern 1 Pattern 2
# Subj 1 3.119196 1.962887
# Subj 2 2.906535 1.754151
# Subj 3 2.915672 1.914559
#
# $mu
# Pattern 1 Pattern 2
# Subj 1 9.519187 4.489174
# Subj 2 9.947885 4.688761
# Subj 3 10.029897 5.418501
#
# $scale
# Pattern 1 Pattern 2
# Subj 1 0.4227306 0.2351866
# Subj 2 0.4058303 0.1622515
# Subj 3 0.3726093 0.1727232
#
# $meanlog
# Pattern 1 Pattern 2
# Subj 1 2.982251 5.007964
# Subj 2 2.878996 4.976754
# Subj 3 3.034019 4.852771
#
# $sdlog
# Pattern 1 Pattern 2
# Subj 1 0.4055664 0.1975062
# Subj 2 0.4172841 0.2115214
# Subj 3 0.4076479 0.1970090Listing 3.7 simulates one (1L) to four (4L) point-patterns (e.g., medical images) for each of the three (3L) subjects (e.g., patients).
set.seed(37); (n = sample(x = 1:4, size = 3L, replace = TRUE))
# [1] 2 3 4Listing 3.8 simulates a grouped hyper data frame with
- one point-pattern (
ppp) hypercolumn, based on the subject-specific parameters in each matrix ofp_Matern(Listing 3.6); and - one-or-more regular columns representing the grouping structure.
r_Matern (Listing 3.5, Listing 3.7)
set.seed(76); r_Matern = p_Matern |>
with.default(expr = {
grouped_rppp(
rMatClust(kappa = kappa, scale = scale, mu = mu),
rlnorm(meanlog = meanlog, sdlog = sdlog),
n = n
)
})
r_Matern
# Grouped Hyper Data Frame: ~g1/g2
#
# 9 g2 nested in
# 3 g1
#
# ppp g1 g2
# 1 (ppp) 1 1
# 2 (ppp) 1 2
# 3 (ppp) 2 1
# 4 (ppp) 2 2
# 5 (ppp) 2 3
# ✂️ --- output truncated --- ✂️3.2.2 with Superimposed Poisson Point-Pattern
Table 3.5 outlines the three steps described in Section 3.2.2,
| To Simulate | Primary Function | |
|---|---|---|
| 1. | subject-specific parameters of (marked) point-patterns, based on multivariate normal distribution, Listing 3.9 | mvrnorm2() (Chapter 47) |
| 2. | number of (marked) point-patterns per subject, Listing 3.7 | base::sample() |
| 3. | grouped hyper data frame with one-and-only-one ppp-hypercolumn, Listing 3.11 |
grouped_rppp() (Chapter 45) |
Consider two superimposed Poisson point-pattern, each with one negative-binomial mark. The population parameters are
- \(x\)- and \(y\)-
coordsby Poisson point-pattern \(\lambda_1=3\), with a negative-binomial mark \((r_1,p_1)=(4,.3)\). - \(x\)- and \(y\)-
coordsby Poisson point-pattern \(\lambda_2=6\), with a negative-binomial mark \((r_2,p_2)=(6,.1)\).
Listing 3.9 also simulate for three (3L) subjects (e.g., patients). The subject-specific parameters deviate from the population parameters under a multivariate normal distribution specified by the standard deviation(s) \(\sigma\) of the subject-specific random effects, i.e., \(\sigma_\lambda=.1\), \(\sigma_r=.2\) and \(\sigma_p=.05\), as well as the restrictions of Table 3.3.
p_Poisson
set.seed(39); p_Poisson = mapply(
FUN = mvrnorm2,
mu = list(lambda = c(3, 6), size = c(4, 6), prob = c(.3, .1)),
sd = list(lambda = .1, size = .2, prob = .05),
MoreArgs = list(n = 3L, row.prefix = 'Subj', col.prefix = 'Pattern'),
SIMPLIFY = FALSE
) |>
within.list(expr = {
lambda = pmax(lambda, .Machine$double.eps)
size = pmax(size, .Machine$double.eps)
prob = pmin(pmax(prob, .Machine$double.eps), 1 - .Machine$double.eps)
})p_Poisson (Listing 3.9)
p_Poisson
# $lambda
# Pattern 1 Pattern 2
# Subj 1 3.059598 5.981443
# Subj 2 2.953268 5.877076
# Subj 3 2.957836 5.957280
#
# $size
# Pattern 1 Pattern 2
# Subj 1 3.807675 5.795670
# Subj 2 3.979154 5.875505
# Subj 3 4.011959 6.167400
#
# $prob
# Pattern 1 Pattern 2
# Subj 1 0.3227306 0.13518657
# Subj 2 0.3058303 0.06225150
# Subj 3 0.2726093 0.07272321Listing 3.11 simulates a grouped hyper data frame using the same grouping size as in Listing 3.7.
r_Poisson (Listing 3.9, Listing 3.7)
set.seed(76); r_Poisson = p_Poisson |>
with.default(expr = {
grouped_rppp(
rpoispp(lambda = lambda),
rnbinom(size = size, prob = prob),
n = n
)
})
r_Poisson
# Grouped Hyper Data Frame: ~g1/g2
#
# 9 g2 nested in
# 3 g1
#
# ppp g1 g2
# 1 (ppp) 1 1
# 2 (ppp) 1 2
# 3 (ppp) 2 1
# 4 (ppp) 2 2
# ✂️ --- output truncated --- ✂️3.2.3 Superimpose Grouped Hyper Data Frames
Listing 3.12 superimposes the simulated grouped hyper data frames r_Matern and r_Poisson (Listing 3.8, Listing 3.11),
(r = superimpose.hyperframe(r_Matern, r_Poisson))
# Grouped Hyper Data Frame: ~g1/g2
#
# 9 g2 nested in
# 3 g1
#
# ppp g1 g2
# 1 (ppp) 1 1
# 2 (ppp) 1 2
# 3 (ppp) 2 1
# 4 (ppp) 2 2
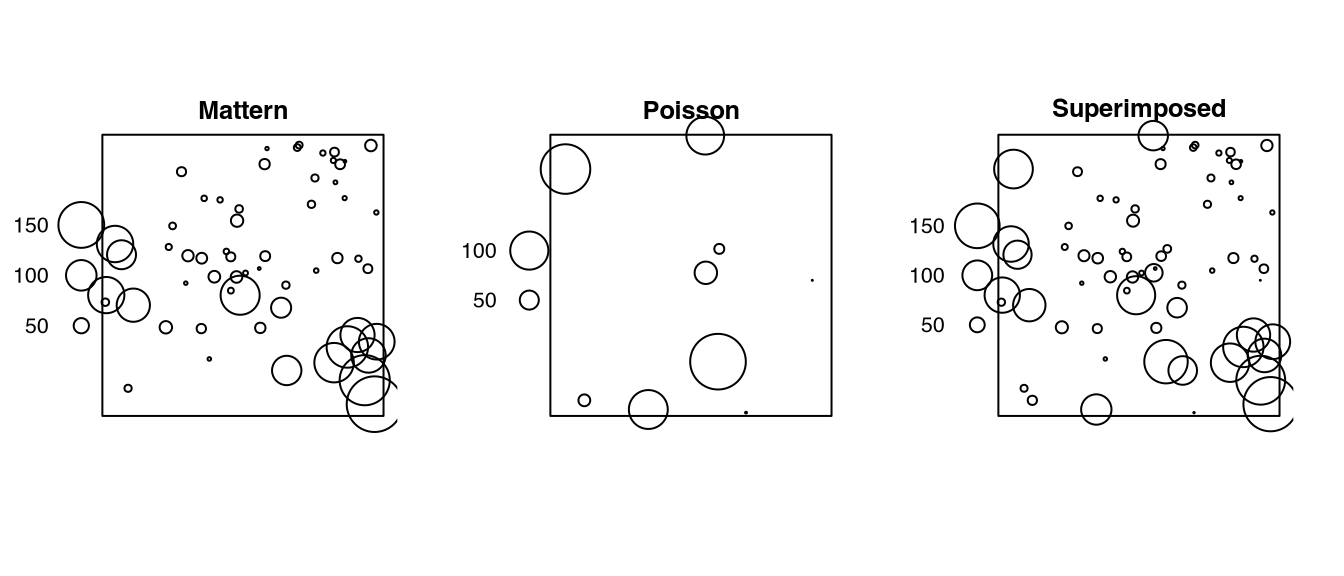
# ✂️ --- output truncated --- ✂️Listing 3.13 checks the return of superimposing (Listing 3.12). Note that the marks may be plotted on different scales.
Code
par(mar = c(0,0,0,0))
z = list(
Mattern = r_Matern$ppp,
Poisson = r_Poisson$ppp,
Superimposed = r$ppp
) |>
.mapply(FUN = spatstat.geom::solist, dots = _, MoreArgs = NULL) |>
do.call(what = spatstat.geom::anylist, args = _)
z[[7L]] |>
spatstat.geom::plot.solist(main = '')